Research Highlight
2025
Effects of the tropical initial state on extratropical forecasts: a scale perspective
The evolution of tropical circulation affects extratropical processes on timescales ranging from days to weeks and beyond. This well-known fact remains an active area of research using observations, reanalysis data, and weather and climate models. The 2025 highlight of the UHH “Atmospheric Dynamics and Predictability” group contributes to this topic by applying a novel modelling framework to estimate the effects of the tropical initial state on extratropical prediction in wave space. The results highlight the initialization of synoptic scales in the deep tropics as key to improving the accuracy of medium-range extratropical forecasts.
A typical method for investigating effects of the initial state (i.e. analysis) in the tropics on the evolution of extratropical prediction in numerical weather prediction (NWP) models is nudging. Nudging replaces temporal evolution of the model over the tropical belt with analyses from the same model, and gradually relaxes the extratropical forecasts towards the tropical analyses within the subtropics. Nudging can be considered a tropical error-denial experiment, as the growth of forecast errors in the extra-tropics is unaffected by processes in the tropics. Nudging also has limitations; it prevents the investigation of dynamical processes within the tropics and subtropics that are influenced by evolving mid-latitude circulation. Nudging prevents the study of the growth of tropical forecast errors or the coupling between the tropics and extra-tropics in NWP forecasts.
The PhD project of Chen Wang applies a novel framework to study the effects of tropical initial state on extratropical forecasts. Named T-OSSE – Tropical Observing System Simulation Experiment, the new framework consists of carrying out data assimilation experiments that assimilate observations exclusively within the tropics. The T-OSSEs can be seen as observation-denial experiments; however, instead of filtering out certain observations types, as in standard OSSEs and observing system experiments (OSEs) with NWP models, T-OSSEs or T-OSEs restrict observations to the tropical belt. Similarly, observations can be limited to the extratopics (M-OSE – midlatitude OSE) or to any latitude belt.
These new type of OSSEs and OSEs have been carried out with the TIGAR model and 3D-Var data assimilation, and, in collaboration with the ECMWF colleagues, with the 4D-Var ECMWF system. The animation in Figure 1 shows analysis differences in the 00 UTC zonal wind at 300 hPa between analyses that assimilated all observations and those that assimilated only observations poleward of 15°S and 15°N. Note occasional appearance of differences along great circles, which are associated with the propagation of uncertainties in tropical analyses from one 12-hour 4D-Var window to the next via the background field.

Figure 1: Differences between the analyses from the ECMWF 4D-Var system assimilating all observations and analyses which assimilates only observations poleward of 15°S and 15°N. The presented variable is the zonal wind at 300 hPa level at 00 UTC. Data assimilation started on 1 December 2022. The horizontal lines run along 15°S and 15°N. Note the nonlinear colourbar scale.
Using T-OSSE with the TIGAR model, Wang et al. (2025) quantified the benefits of assimilating observations in the tropics (i.e. the tropical initial state - TIS) for 30-day forecasts in terms of normalized mean square forecast errors across different wavenumbers along the latitude circles, denoted T-score. Negative values of the T-score in Figure 2 denote percentages of forecast improvements relative to the case without the assimilation of tropical observations. At forecast day 0, the T-score is zero everywhere except in the immediate vicinity of the 15°S and 15°N latitudes, where observations are still available, and the background-error covariances spread the observational impact somewhat meridionally. The propagation of TIS effects to higher latitudes during the forecasts is scale dependent. While TIS effects are found in the subtropics at all scales after 10 days of forecasts, the effects at sub-synoptic scales do not spread to the poleward side of the jets (north of 35°N and south of 46°S. In contrast, TIS effects at the synoptic scales extend into the polar regions after 10 days, reaching 700 and beyond.

Figure 2: The T-score as a function of zonal wavenumber and latitude for Rossby wave zonal wind at forecast lead times 5, 10, 15, 20, 25, and 30 days. The horizontal orange lines mark the latitudes of the maximal zonal mean zonal wind (jet cores). The vertical red lines separate planetary scales (0 ≤ k ≤ 4), synoptic (3 ≤ k ≤ 15), and sub-synoptic scales (k ≥ 14).
The scale-dependency of TIS effects on the extra-tropics can be explained by the way spherical signals propagate from one latitude to another using the theory of Rossby wave propagation in a barotropic atmosphere developed by Hoskins and Karoly (1981). At each latitude, the theory provides a stationary (or turning) wavenumber, Ks, at which the meridional group velocity of Rossby waves becomes zero. All waves with scales smaller than this turning scale cannot propagate poleward beyond their turning latitude. The application of Rossby wave theory agrees well with the observed behaviour in the T-OSSEs.
Another perspective on scale effects is presented in Figure 3, which shows the evolution of the T-score for different scales. It demonstrates that the TIS effects at larger synoptic scales (3 < k < 9, where k is the zonal wavenumber) propagate poleward fastest. This can be understood by considering the meridional group velocity of Rossby waves, vg , and identifying the zonal wavenumber for which vg is maximized, which is l/sqrt(3), where l is the meridional wavenumber; g then decreases monotonically as a function of |k - kmax |. Since extratropical dynamics is dominated by synoptic meridional scales, this shows that the fastest propagating signals are at the largest zonal synoptic scales.
Even if sub-synoptic scales in the tropics cannot directly affect mid-latitude forecasts, could they do so via scale interactions that propagate small-scale effects to larger scales? This question can be addressed by retaining in the initial state only the effects of observations within a selected scale range. The results show that an inverse cascade effect of TIS from small scales to synoptic scales does take place, but this process competes with the forward cascade of synoptic-scale effects to smaller scales. Given the redness of the analysis-error variance spectrum, it is questionable whether even perfect small-scale initial conditions in the tropics play a significant role for forecasts outside the tropics. Ongoing analysis of T-OSE and M-OSE experiments with the ECMWF model will provide further insights into the role of scale interactions in 3D NWP forecasts.

Figure 3: The T-score as a function of the forecast lead time and latitude at (a) planetary scales (1 ≤ k ≤ 3), (b) larger synoptic scales (4 ≤ k ≤ 8), (c) smaller synoptic scales (9 ≤ k ≤ 14), and (d) larger sub-synoptic scales (15 ≤ k ≤ 20).
This research was funded by UHH and by the DFG Grant 461186383. Chen Wang was also supported by the CRC TRR181 graduate school “ENERGY” funded by the DFG Grant 274762653.
Reference:
Wang, C., N. Žagar, and S. Vasylkevych, 2025: On the Effects of the Tropical Initial State on Extratropical Forecasts: A Scale Perspective. Mon. Wea. Rev., 153, 2069–2083, https://doi.org/10.1175/MWR-D-25-0009.1
2024
New theory for the generation of mixed Rossby-gravity waves
The mixed Rossby-gravity (MRG) waves (Figure 1) are known to contribute significantly to tropical variability; therefore, understanding their generation is important for the predictability of tropical weather. However, earlier theories of the MRG excitation could not explain the scale selection.
Maho et al. introduced a new theory of the MRG wave excitation that leads to the MRG waves with horizontal scales that correspond to the synoptic scales observed in the tropical upper troposphere. The key aspect of the new theory is the interaction between waves emanating from tropical heat sources and an asymmetric subtropical zonal jet.
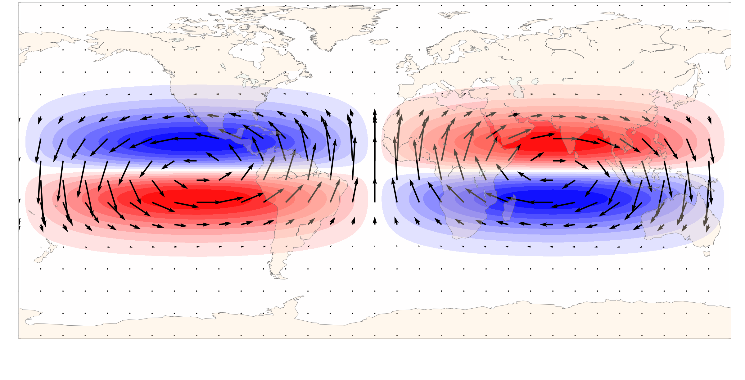
Figure 1. Horizontal structure of the winds and geopotential height perturbations of zonal wavenumber 1 spherical MRG wave. Positive and negative geopotential height is shown by red and blue shades. From https://modes.cen.uni-hamburg.de/Hough#part2.
The new mechanisms was derived using idealized simulations with the Transient Inertia-gravity and Rossby wave dynamics (TIGAR) model which solves the rotating shallow water (RSW) equations on the sphere using Hough harmonics (https://modes.cen.uni-hamburg.de/Hough) as spectral expansion basis, thereby representing MRG waves as prognostic variables. The simulations involved a tropical heat source mimicking convection and a geostrophically balanced zonal background flow comprising of symmetrical and asymmetrical jets (Figure 2). By asymmetry, we mean that the flow field has asymmetric component with respect to the equator. In addition, we applied a linear TIGAR model, which solves the RSW equations linearized around the zonal background flow. The tropical heat source generates a spectrum of Rossby and inertia-gravity waves that interact with the asymmetric jet, and this gives rise to MRG waves. Presence of asymmetry in the background flow was shown to be crucial for the MRG wave generation (Figure 3).
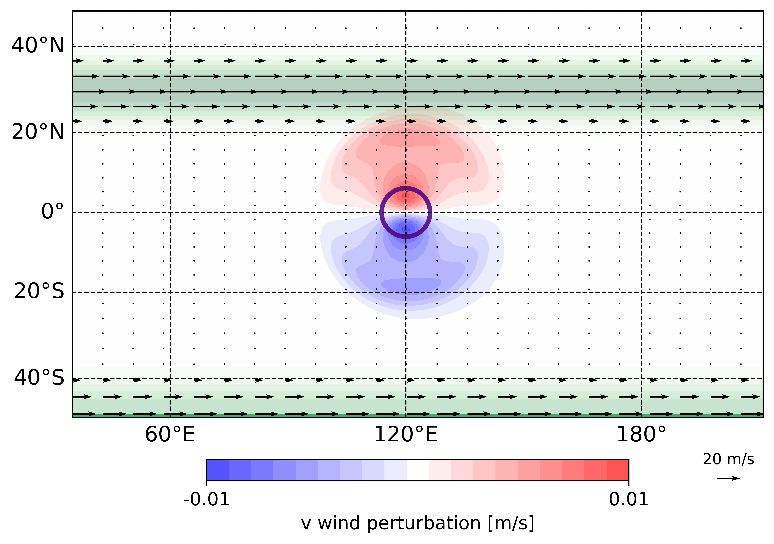
Figure 2. Snapshot of an idealized TIGAR global simulation run with a tropical heat source (purple circle). Red and blue shading denote the meridional wind perturbations (i.e. waves generated by the heat source). Shades of green and the arrows denote the background flow (asymmetric subtropical jet structure).
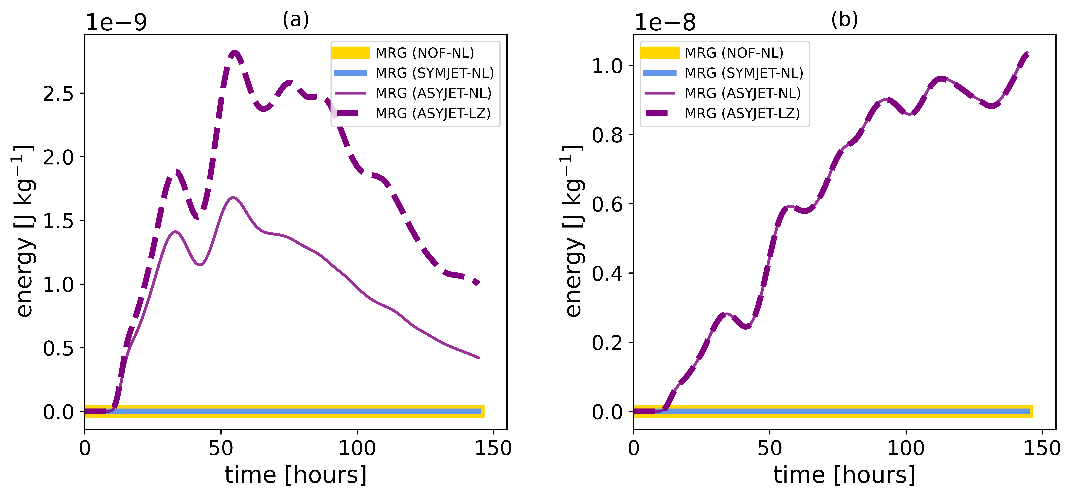
Figure 3. Evolution of MRG wave energy in the idealized TIGAR simulations (a) with damping and (b) with no damping. MRG waves grown only in the linearized (LZ) and non-linear (NL) simulations using asymmetric jet (ASYJET) as background flow. Background flows of symmtric jet (SYMJET) and no mean flow (NOF) do not produce MRG waves.
We quantified dynamical factors contributing to MRG wave tendencies among forcing by the asymmetric heat source, wave-wave and wave-mean flow interactions (Figure 4). We show that the impact of wave-wave interactions is small compared to the effect of wave-mean flow interactions and the asymmetric forcing. The spectrum of absolute MRG wave tendency by wave-mean flow interactions has a peak at large scales, whereas the forcing spectrum appears to be flat across large scales, which shows us that wave-mean flow interactions are responsible for the MRG wave scale selection
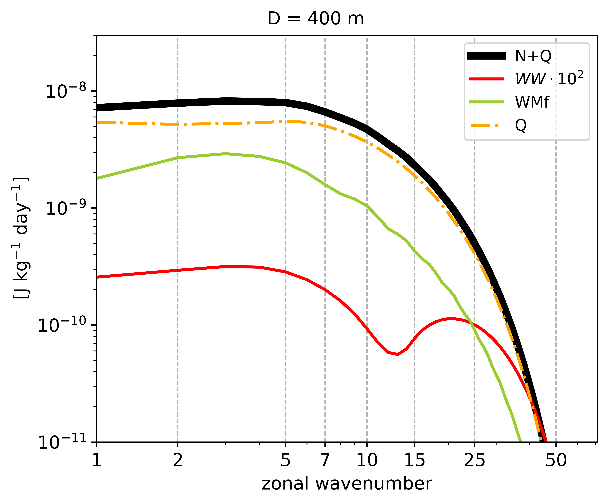
Figure 4. Spectra of absolute tendency of MRG waves decomposed into contribution by the forcing (Q), wave-mean flow (WMf) and wave-wave (WW) interactions. The total absolute MRGW tendency spectrum (N+Q) is shown by the thick black curve.
The results from simulations with idealised background flows was confirmed by simulations using realistic background zonal winds derived from ERA5 reanalysis data. We found that the larger the asymmetry the larger the MRG wave amplitude (Figure 5) irrespective of the symmetry of the tropical heat source. The simulations with realistic background profiles produced MRG waves with the observed (synoptic) scales.
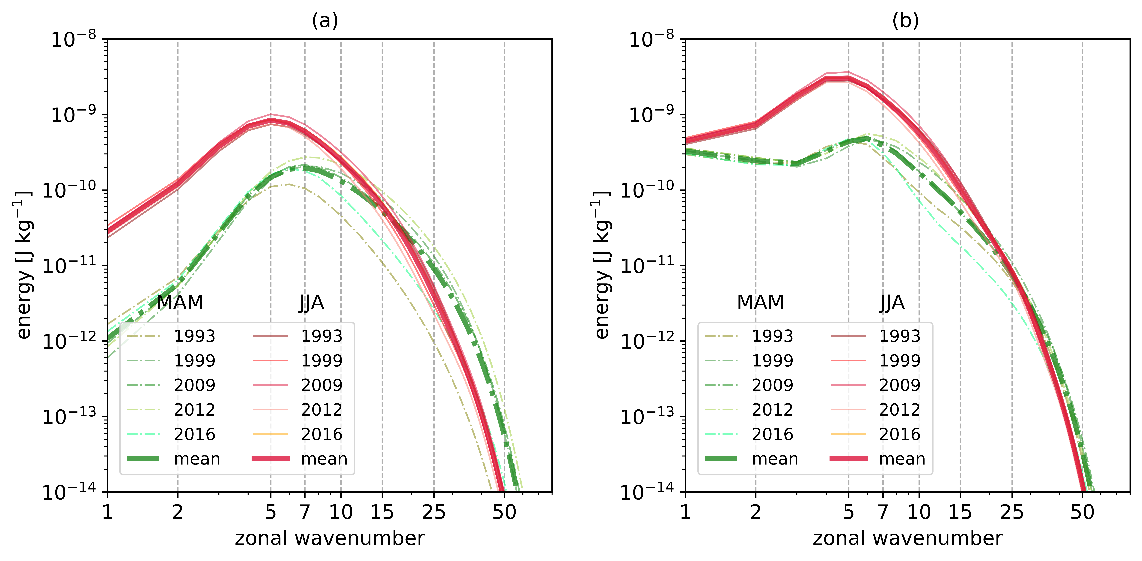
Figure 5. MRG wave energy spectra in the TIGAR simulations using realistic background flows derived from the zonally averaged zonal wind of 200 hPa from ERA5. (a) Symmetric heat source, (b) asymmetric heat source. Shades of green and red show simulations using background flows of MAM and JJA respectively. JJA flows have higher zonal asymmetry.
This work is part of the DFG-funded project TRR181 “Energy transfers in atmosphere and ocean”.
Reference:
Mahó, S. I., S. Vasylkevych, and N. Žagar, 2024: Excitation of mixed Rossby-gravity waves by wave - mean flow interactions on the sphere. Quart. J. Roy. Met. Soc.. DOI: 10.1002/qj.4742.
2023
How white is the sky?
We have derived the limit spectra of the kinetic energy of vertical motions in the hydrostatic atmosphere and applied it to reanalysis data. This project has been ongoing since 2018, and it is since 2020 funded by the DFG within the TRR181 “Energy transfers in the atmosphere and ocean” project.
Within the project, we have extended the linear normal-mode function (NMF) theory to the unified computation of vertical velocities associated with the Rossby waves and inertia-gravity (IG) waves, and their zonal wavenumber kinetic energy spectra (i.e. vertical kinetic energy, or VKE, spectra). In the same framework, we have developed a new approach to the computation of the zonal wavenumber spectra of the kinetic energy of horizontal velocities (i.e., horizontal kinetic energy, HKE, spectra). The decomposition of both horizontal and vertical motions in terms of the Rossby and gravity waves within the same framework provides a consistent comparison of the zonal wavenumber horizontal and vertical energy spectra for the two regimes.
The full derivation can be found in J. Atmos. Sci. paper, https://doi.org/10.1175/JAS-D-23-0090.1. The AGU 2022 talk is here.
New theoretical developments show that for every zonal wavenumber k, the limit VKE is proportional to the total mechanical energy and to the square of the frequency of the normal mode. The theory predicts a VKE ∝ k-5 and a VKE ∝ k1/3 power law for the Rossby and IG waves, assuming a k-3 and a k-5/3 power law for the Rossby and IG HKE spectra, respectively. The Kelvin and mixed Rossby-gravity wave VKE spectra are predicted to follow k-1 and k-5 power laws, respectively (Table 1).
The latitude-by-latitude and level-by-level HKE and VKE spectra applied to the ERA5 reanalysis data expose major latitudinal and seasonal variations i.e., anisotropy of both the horizontal and vertical energy distribution. The ERA5 data does not have an adequate resolution or representation of gravity waves. Therefore, the theoretical k1/3 power law for the IG VKE spectrum is found only in the stratosphere for k ≈ 10-60.
The inertial range IG VKE spectra in the tropical and midlatitude troposphere reflect a mixture of ageostrophic and convection-coupled dynamics and have slopes between -1 and -1/3, likely associated with too steep IG HKE spectra. The forcing by quasi-geostrophic ageostrophic motions is seen as an IG VKE peak at synoptic scales in the upper troposphere which gradually moves to planetary scales in the stratosphere.
The regime decomposition of vertical velocity paves the way for the decomposition of the vertical momentum fluxes due to the Rossby waves, IG waves, the Kelvin and mixed Rossby-gravity waves across scales that are currently being completed. For more details on this, contact Valentino Neduhal.
Table 1: Scaling laws for the frequency, the total mechanical energy I (sum of the kinetic energy of horizontal motions and available potential energy) and the vertical kinetic energy (E) as a function of the zonal wavenumber k. The wavenumber index k is used for the large scales tropical flows where both k and meridional mode index n are small.
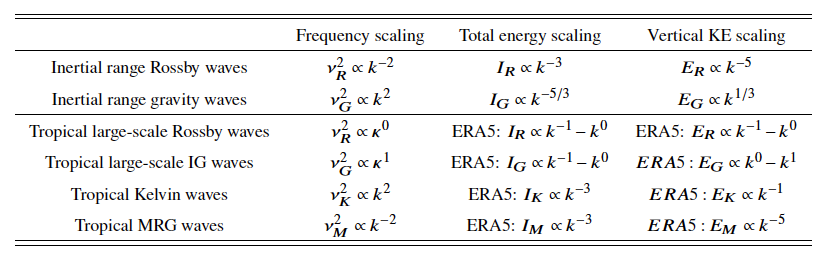
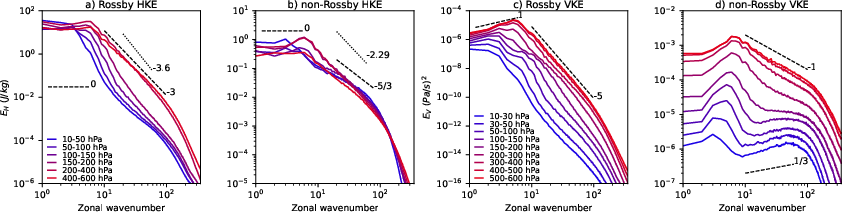
Figure 1: (a)-(b) The horizontal and (c)-(d) vertical kinetic energy of (a), (c) Rossby and (b), (d) non-Rossby motions in the latitude belt 30°S-60°S in different layers, as indicated in the legend. Spectra are averaged for the ERA5 data in August 2018. Note that non-Rossby modes consist only of the IG modes in the extratropics. Adapted from https://doi.org/10.1175/JAS-D-23-0090.1
Reference:
Žagar, N., V. Neduhal, S. Vasylkevych, Ž. Zaplotnik, and H. L. Tanaka, 2023: Decomposition of Vertical Velocity and Its Zonal Wavenumber Kinetic Energy Spectra in the Hydrostatic Atmosphere. J. Atmos. Sci., 80, 2747–2767, https://doi.org/10.1175/JAS-D-23-0090.1.
